On Some Language Extension of Logic MR: A Semantic and Tableau Approach

Abstract

In the article we present an extension of the minimal, normal positional logic, i.e., the logic with realization operator MR. Positional logic is a philosophical logic that makes it possible to relate sentences to contexts that can be understood in many ways. We enrich the basic language of minimal positional logic with additional expressions built with predicates and positional constants. We also accept expressions built with the realization operator and many positions, like:

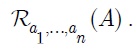
Thanks to this, we increased the expressivity of minimal positional logic. In the article we point to many examples of the fact that, thanks to this small change, complex theories based on the proposed extension can be created. As a theory of proof for our logic, we assume tableau methods, showing soundness and completeness theorems. At the end, however, we show that the logic studied here is only a language extension of the MR: all theorems of the extension have their equivalents in pure MR theorems. However, theories built upon the proposed extension can express much more than theories built upon pure MR.